In this article, I'll use some basic machine learning methods to train a bot to play cards against me. The card game that I'm interested in is called Literature, a game similar to Go Fish.
- GitHub repo for game engine: https://github.com/neelsomani/literature
- GitHub repo for React web app: https://github.com/neelsomani/literature-server
The version of Literature that I implemented is similar to the rules I linked above. Literature is played in two teams, and the teams compete to collect "sets." A set is a collection of either A - 6 of a suit or 8 - K of a suit (7's are not included in the game).
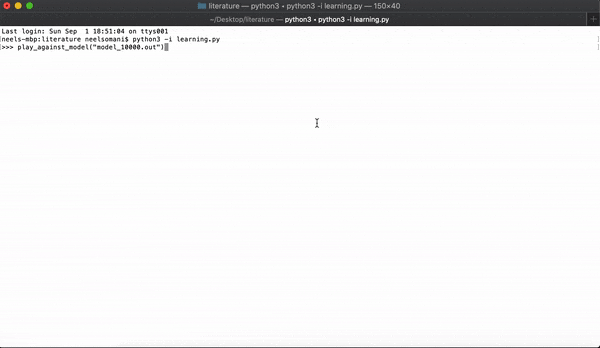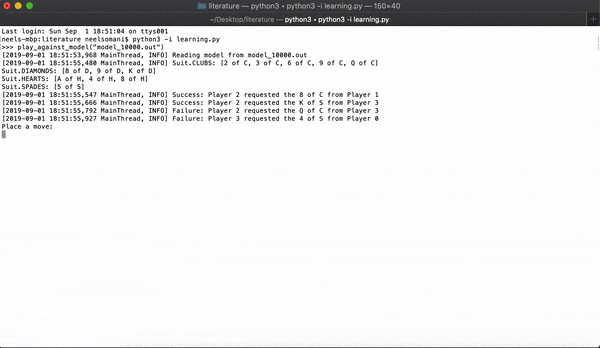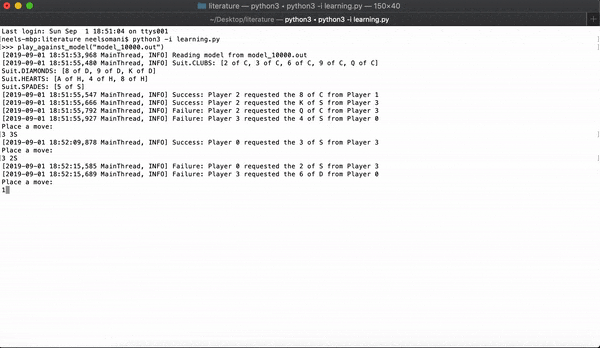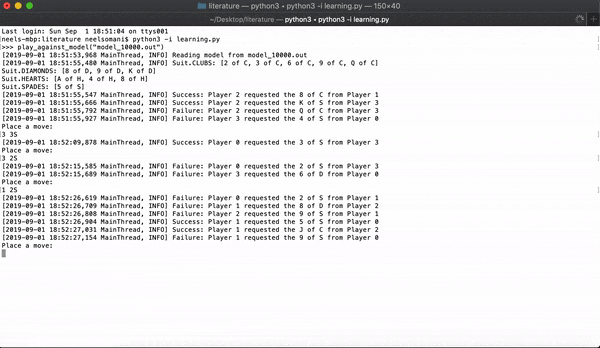
When it's a player's turn, they can ask anyone from the opposing team for a card from one of the sets. The player who asks must already have at least one card in the set, and they cannot ask for a card that they already have. For example, if a player asks for a 4 of hearts, that implies they either have the A, 2, 3, 5, or 6 of hearts. If the other player has the card, they hand it over and the asking player gets another turn. If the other player doesn't have the card, now it's their turn.
To claim a set, a team must possess all of the cards from a set, and any player from the team needs to name each of the members of their team who has each card. Whichever team claims the most sets wins.
I'm interested in Literature because I couldn't find any online implementations of it (so there definitely weren't any existing bots), and I wanted to play the game myself.
Approach
Model
I decided to approach the problem with a modified version of Q-learning. In Q-learning, a model attempts to learn the rewards associated with any given (state, action) pair. For a given state, it picks the action that maximizes the reward.
I didn't do Q-learning exactly as specified. I made a few changes:
- I used a neural net to learn the rewards, rather than storing a matrix of every (state, action) pair. That's because the serialized game state (described below) is fairly large.
- There isn't any points system built into this game, so for the reward, I just associated a positive constant as the reward for winning a game and a negative constant as the penalty for losing a game.
- I ended up assigning the positive reward for every single (state, action) pair for the winning team and the negative reward for every (state, action) pair for the losing team. My justification for this is that over a large enough number of games, "good" moves should appear in winning games with higher probability than "bad" moves, so on average good moves should end up with higher rewards. (That probably requires an intractably large number of training games to be true in practice.)
Defining the game state
I defined a player's game state in five parts:
- The "player number" for this particular player: \(0, \dots, n - 1\) where \(n\) is the number of players;
- A serialized representation of each player's hand - specifically, whether a given player definitely does, definitely does not, or could possibly possess each card;
- The minimum number of cards that a given player must possess in each suit;
- The number of cards each player has;
- What this player knows that other players know about each other. (For example, if Player A successfully asks Player B for a 4 of hearts, all of the other players know that now Player A definitely has the 4 of hearts and at least one other heart, and that Player B definitely does not have the 4 of hearts.)
While there might be a more compact way of representing this information, each of those five parts do add information (i.e., you can't derive the fifth one if you only know the other four).
To calculate the game state, I implemented a set of inference rules. For example, if a player definitely possesses a card, then all other players definitely do not possess that card. A more complicated example: if a player has only one card and asks for a card in a particular half suit, then the player definitely does not possess any cards in all other half suits.
Solving the Problem Efficiently
I had to impose some limitations to make this training process work in practice.
Speeding up the training process
I initially had the bots pick a move over all possible valid moves (where a "valid" move is a move that doesn't violate the rules of the game). The bots were just taking way too long to finish a single game, so I had to help them out.
Instead, I made them prioritize asking a player for a card if the other player either definitely had or possibly had the card. In other words, the model would never request a card from a player if the player definitely doesn't have that card, unless there are no other valid moves. That's not always desirable, because sometimes you might want to deliberately ask for a card that someone doesn't have to give your teammates some information - for example, the information that you don't have the card you requested, but you do have another card in the set.
Another fix I made to speed up the process was killing games that were taking longer than 200 moves. More often than not, the bots were getting caught in a loop of repeatedly (unsuccessfully) requesting the same cards in those cases.
Avoiding local optima
To avoid bots getting caught in a loop of asking each other for the same cards repeatedly, I added some unit normal noise to the outputted reward, so occassionally a seemingly suboptimal move would be made. I also started giving a minor reward to moves that resulted in successfully receiving a card, and a minor penalty to moves that failed to receive a card.
Measuring Success
I trained a model with the method above for 10,000 games on an AWS EC2 c5d.2xlarge instance. I had 8 threads running games concurrently. It took about a day ($25).
Competing a trained model vs. an untrained model
The most obvious test is to see whether the trained model beats the untrained model with some degree of significance. For 1500 games, the trained model won 827, the untrained model won 346, and the models tied 327 games. Even without any formal statistical reasoning, that's evidence that the trained model is substantially better than the untrained model.
The average length of games between two untrained models vs. the average length of games between a trained and untrained model is also informative. If the untrained model is actually worse, we'd expect the games to be shorter against the trained model, since the trained model's moves are less random and more strategic, resulting in quicker game outcomes.
For 1500 games, the average length of a game for two untrained models was about 77.8, while the average length of a game for a trained vs. untrained model was 75.1. To see whether that discrepancy of 2.7 was significant, I mixed together the game lengths of the trained vs. untrained and untrained vs. untrained model games. Then I randomly sampled two groups of 1500 game lengths and calculated the difference in their average game length, 1000 times. Not once in the 1000 samples did the difference exceed 2.7, so it is a significant discrepancy.
Evidence of strategy
I wanted to see if the trained model learned any undeniably "good" sequences of moves. Here's a common scenario: a player takes a card from you (say, the A of hearts), then fails to take another card (maybe the 2 of hearts). Now it's your turn and the other player has given you a lot of information:
- It's usually optimal to ask for the card that was taken from you back if you can (although it reveals that you still have another heart)
- If you now have enough info to claim the entire suit, it is always optimal to do so
I wanted to see whether the trained model was more likely to make these strategic moves.
In the 1500 untrained vs. untrained model games, the models asked for a card back immediately after it was taken 573 times. They claimed the entire set 95 times. In the 1500 trained vs. untrained model games, the models asked for a card back immediately after being taken 1533 times, and they claimed the entire set 468 times. So it looks like the trained model games involved more strategy than the untrained model games.
Average number of moves during training
Over the course of the 10,000 training games, the number of moves per game should decrease, since the model should make more strategic moves and therefore have quicker claims (and game outcomes). The average length of the first 1000 games was 86.58 moves, while the average length of the last 1000 games was 75.98 moves.
Subjective evaluation
The bots beat me, but to be fair, I'm not very good at the game. That's the reason why I made the bots to begin with.
Conclusion
I hope this was informative. Feel free to let me know if you have any questions. I'm interested to see how well this method would adapt to playing games like poker.
