My brother recently introduced me to the show "Are You the One?" From the Wikipedia page:
A group of men and women are secretly paired into couples by producers, via a matchmaking algorithm. Then, while living together, the contestants try to identify all of these "perfect matches." If they succeed, the entire group shares a prize of up to $1 million.
They're given two major pieces of information:
- Each week, the contestants guess what the correct pairs are. They're shown some number of lights, which represents how many pairs they got correct.
- The contestants can send one couple to the "truth booth" each week, which tells them whether those contestants are certainly together or certainly not together.
So after \(k\) weeks, we have:
- \(N\) actors: \(a_{1}, ..., a_{N}\)
- \(\frac{N}{2}\) unknown correct pairs: \((a_{i_{1,1}}, a_{i_{1, 2}}), ..., (a_{i_{\frac{N}{2}, 1}}, a_{i_{\frac{N}{2}, 2}})\)
- \(k\) groups of couples (each of which I'll call a "pairing") and the number of lights they produced for each week
- \(m\) pairs that MUST be in the solution (went to the truth booth successfully): \((a_{j_{1,1}}, a_{j_{1,2}}), ...\)
- \((k - m)\) pairs that must NOT be in the solution (went to the truth booth unsuccessfully)
What's the probability of each pair being together? What's the optimal strategy? If you want to try out the code yourself, you can check it out here: https://github.com/neelsomani/are-you-the-one
All of the results in this blog post are in the examples.py file.
Here's what the probability matrix looks like for this week (season 8, week 6):
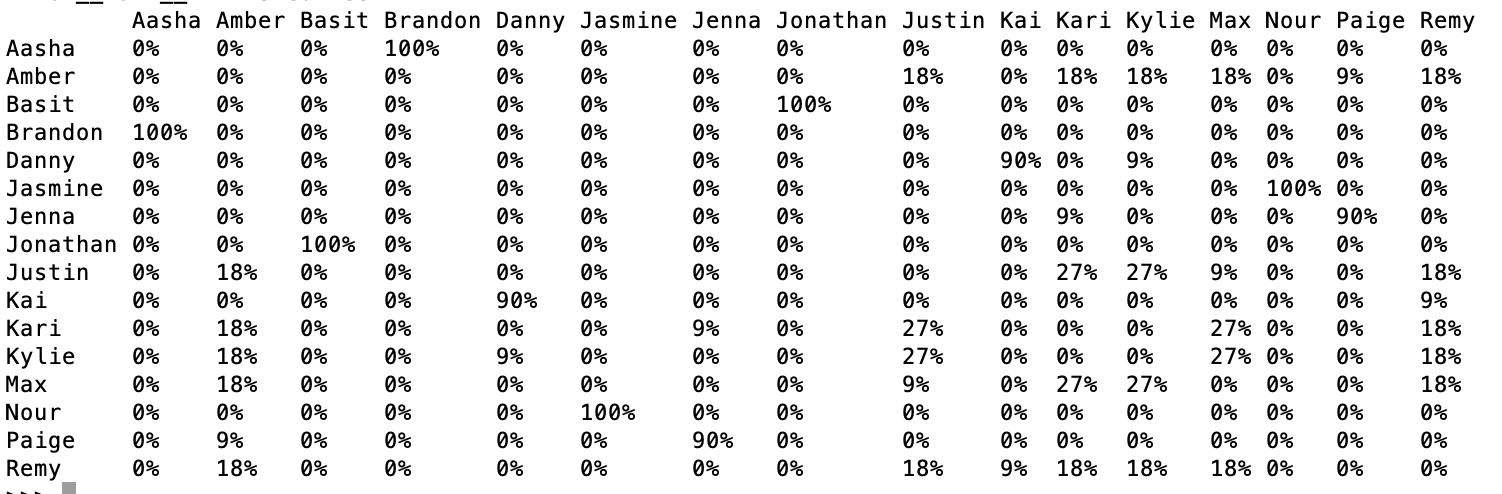
Note that while Jasmine and Nour haven't been in the truth booth, they must be each others' perfect match. Jenna and Paige have about a 90% chance of being each others' perfect match. I rounded the numbers for the visualization. There are only 11 possible pairings at this point in the season.
I'll outline some of the results below.
Defining the Solution Space
A "pairing" is a mapping of each contestant to another contestant. The mapping is symmetric and one-to-one.
A pairing is "valid" if the pairing does not violate the constraints above. That is, for each week, if that pairing were the truth, it should have produced the observed number of lights. The pairs that must be together are paired in a valid pairing, and no pairs that cannot be together are paired.
To simplify the notation: We'll denote a pairing with \(P\), where \(P\) is a set that contains \(\frac{n}{2}\) pairs of actors of the form \((a_i, a_j)\). The set of valid pairings is \(V\). We'll let \(P^*\) be the correct pairing, a random variable such that \(\Pr[P^* = v] = \frac{1}{|V|}\). We'll let \(L(P | P^*)\) be the number of lights produced for a pairing \(P\) given the correct pairing \(P^*\).
The probability of a couple being together is the number of valid pairings where the couple is together, divided by the total number of valid pairings: $$\Pr[(a_{i}, a_{j}) \in P^*] = \frac{|\{P \in V | (a_{i}, a_{j}) \in P\}|}{|V|}$$
Or in general, the probability of any predicate \(C\) being true for the correct pairing:$$\Pr[C(P^*)] = \frac{|\{P \in V | C(P)\}|}{|V|}$$
Since in this season, no one has any gender preference, any of the candidates could have been with anyone else a priori. That means there are initially \(\frac{16!}{8! * 2^8}\) valid pairings. In the case of gender preferences, we can incorporate that information in the same way as above. For example, a group of straight men can be defined as a group of people that cannot be paired with each other. By converting this group into a list of pairs (the Cartesian product of the group with itself), we can treat them the same way as couples who went into the truth booth and were confirmed not to be matches.
Here's what the probability matrix looked like for season 7, episode 4:
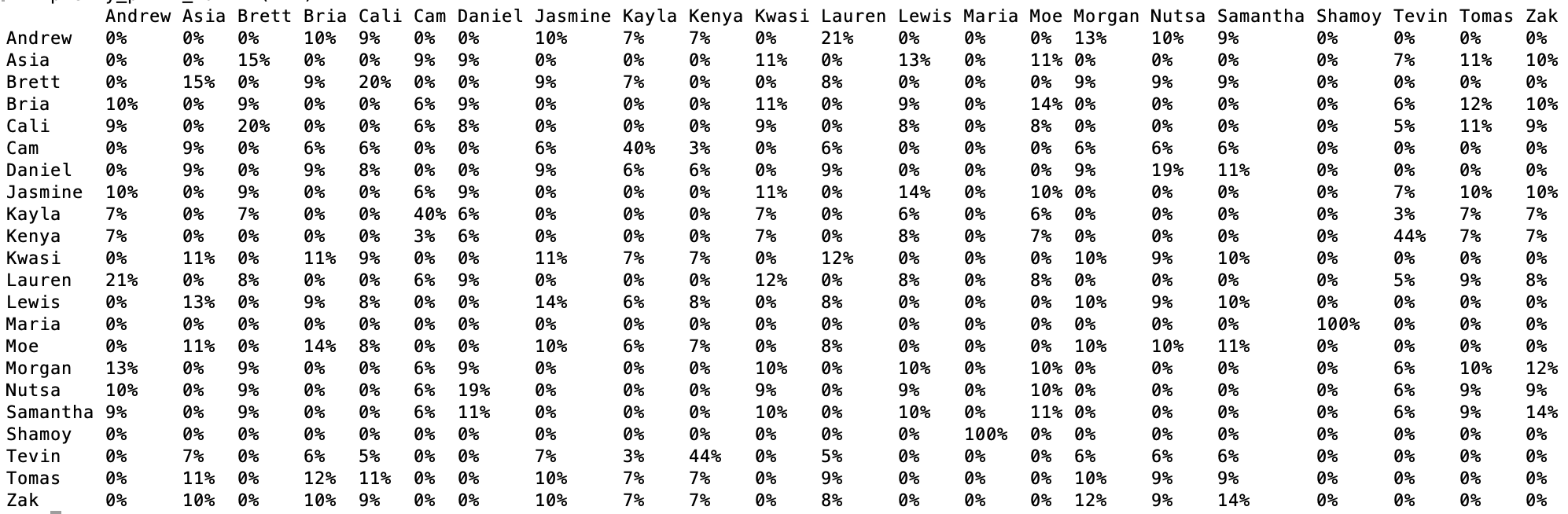
Defining Optimality
Let's define optimality as a move that minimizes the size of the solution space in expectation. For example, a move that doesn't shrink the size of the solution space gives us no information and is therefore suboptimal. A move that shrinks the solution space down to a single possible pairing is as good as it gets.
Optimal play for the truth box
For the truth box, the contestants should send the pair that is the closest to a 50% chance of being a match. This is because that probability minimizes the size of the solution space in expectation.
Specifically, if actors \(a_{i}\) and \(a_{j}\) are a match in \(p\) proportion of the solutions, then the expected number of valid pairings after sending them to the truth box is \(p * p * N + (1 - p) * (1 - p) * N\), where \(N\) is the original number of valid pairings. This is because \(p\) of the time you'll end up with \(p * N\) valid pairings left, and \((1 - p)\) of the time you'll have \((1 - p) * N\) pairings left. Minimizing with respect to \(p\), you'll find that \(p = .5\) is the optimal proportion.
Optimal play for the pairings
Unfortunately I wasn't able to fully solve the pairings this afternoon. To pick the optimal guess \(\hat{P}\) for a single move, you could minimize the expected number of remaining valid pairings over the distribution of the number of lights you might see:
$$\hat{P} = \textrm{argmin}_{P} \sum_{k} \frac{|\{v \in V | L(P | v) = k\}|^2}{|V|}$$
$$ = \textrm{argmin}_{P} \sum_{k} |\{v \in V | L(P | v) = k\}|^2$$
That gives us a greedy algorithm to pick the optimal guess one move at a time. In reality, we would want to make the series of guesses that minimizes the expected number of valid pairings after ALL guesses, not just the next one. Regardless, under this framework, the optimal guess for this week would be:

Actually, this is one of a few equally optimal guesses for this week.
Solving the Problem Efficiently
The solution in the image above isn't quite correct, because I only looked across the valid pairings, not all pairings. I suspect that the \(\hat{P}\) that minimizes the equation above would be in \(V\), but I wasn't able to formally prove that today, and I'm really not sure that it's even true. One motivation is that:
$$\textrm{argmin}_{P} \sum_{k} { |\{v \in V | L(P | v) = k\}|^2 }$$ $$= \textrm{argmin}_{P} \sum_{k} \frac{|\{v \in V | L(P | v) = k\}|^2}{|V|^2}$$$$= \textrm{argmin}_{P} \sum_{k} \Pr[L(P | P^*) = k]^2$$
This equation is subject to the constraint: $$\sum_{k} \Pr[L(P | P^*) = k] = 1$$
which, by the method of Lagrange multipliers, shows that the best possible guess would have an equal chance of having any number of lights: $$\Pr[L(P | P^*) = k] = \frac{1}{\frac{N}{2} + 1}$$ That solution definitely doesn't exist in general, since \(\Pr[L(P | P^*) = \frac{N}{2} - 1] = 0\) (you can't have only one pair mismatched) and \(\Pr[L(P | P^*) = \frac{N}{2}] = \frac{1}{|V|}\) iff \(P \in V\) (0 otherwise). The next best thing would be to make the remaining number of lights all equally likely, which would give a slightly lower expectation for a valid pairing.
Note that this also shows that if such an optimal guess existed (such that \(\Pr[L(P | P^*) = k] = \frac{1}{\frac{N}{2} + 1}\)), minimax would have yielded the solution. Since no such solution exists, there are times when minimax will not minimize the size of the solution space in expectation. For example, if there were only six contestants, then minimax would prefer a guess \(P\) with:
$$\Pr[L(P | P^*) = 0] = .35$$ $$\Pr[L(P | P^*) = 1] = .35$$ $$\Pr[L(P | P^*) = 2] = .29$$ $$\Pr[L(P | P^*) = 3] = .01$$
over:
$$\Pr[L(P | P^*) = 0] = .36$$ $$\Pr[L(P | P^*) = 1] = .32$$ $$\Pr[L(P | P^*) = 2] = .31$$ $$\Pr[L(P | P^*) = 3] = .01$$
since the worst case for the latter would leave 36% of the possibilities, but the worst case for the former would leave 35%. But the latter distribution minimizes the size of the solution space in expectation.
Conclusion
I hope that this added some insight into the show. Feel free to let me know if you need help using the linked code to do your own analysis.
